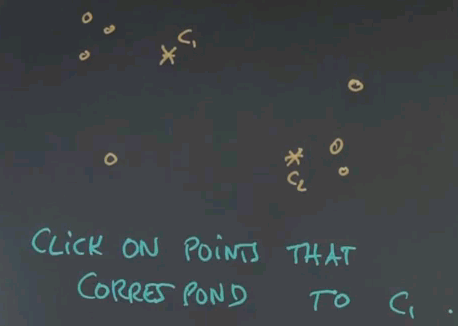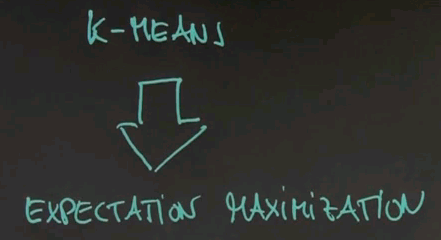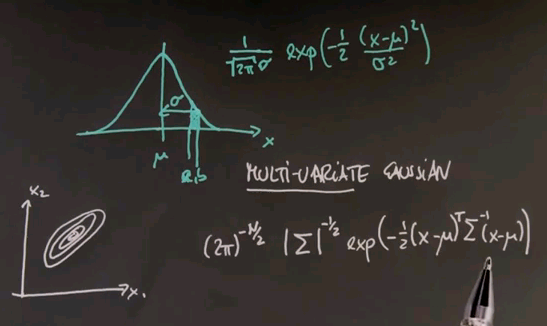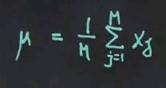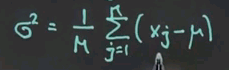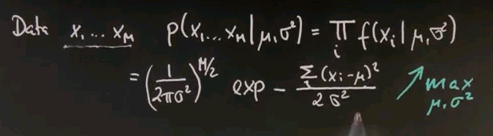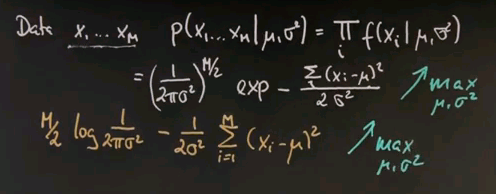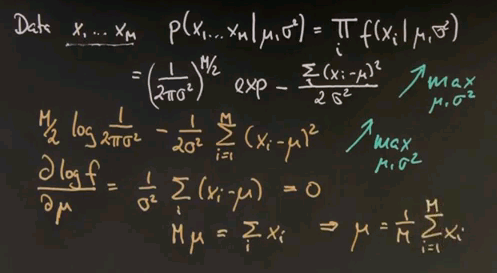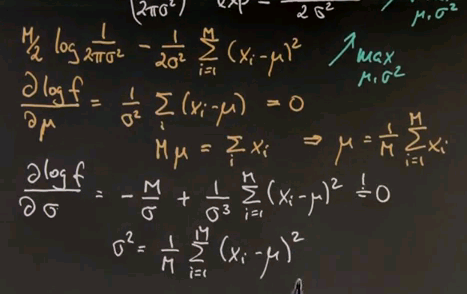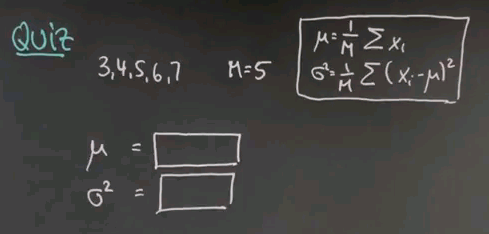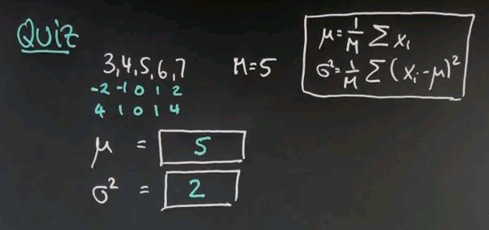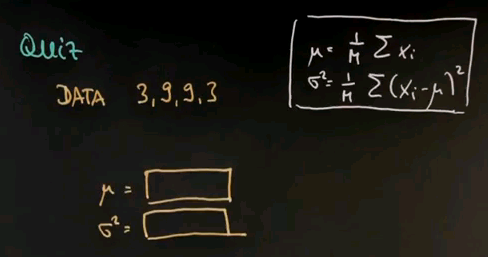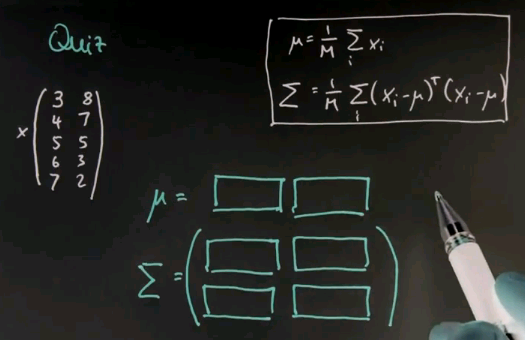These are my notes for unit 6 of the AI class.

Unsupervised Learning

So welcome to the class on unsupervised learning. We talked a lot about supervised learning in which we are given data and target labels. In unsupervised learning we're just given data. So here is a data matrix of data items of n features each. There's m in total.

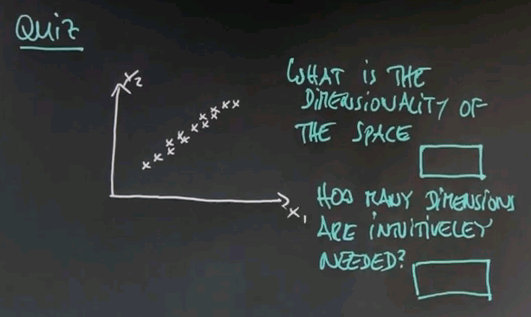
So the task of unsupervised learning is to find structure in data of this type. To illustrate why this is an interesting problem let me start with a quiz. Suppose we have two feature values. One over here, and one over here, and our data looks as follows. Even though we haven't been told anything in unsupervised learning, I'd like to quiz your intuition on the following two questions: First, is there structure? Or put differently do you think there's something to be learned about data like this, or is it entirely random? And second, to narrow this down, it feels that there are clusters of data the way I do it. So how many clusters can you see? And I give you a could of choices, 1, 2, 3, 4, or none.

The answer to the first question is yes, there is structure. Obviously these data seem not to be completely randomly determinate. There seem to be, for me, two clusters. So the correct answer for the second question is 2. There's a cluster over here, and there's a cluster over here. So one of the tasks of unsupervised learning will be to recover the number of clusters, and the centre of these clusters, and the variance of these clusters in data of the type I've just shown you.

Question

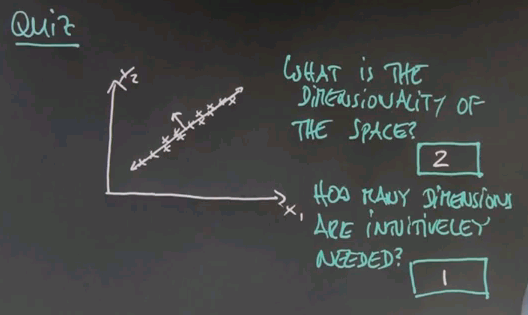
Let me ask you a second quiz. Again, we haven't talked about any details. But I would like to get your intuition on the following question. Suppose in a two-dimensional space all the data lies as follows. This may be reminiscent of the question I asked you for housing prices and square footage. Suppose we have two axes, x₁ and x₂. I'm going to ask you two questions here. One is what is the dimensionality of this space in which this data falls, and the second one is an intuitive question which is how many dimensions do you need to represent this data to capture the essence. And again, this is not a clear crisp 0 or 1 type question, but give me your best guess. How many dimensions are intuitively needed?

And here are the answers that I would give to these two questions. Obviously the dimensionality of the data is two, there's an x dimension and a y dimension. But I believe you can represent this all in one dimension. If you pick this dimension over here then the major variation of the data goes along this dimension. If you were for example to look at the orthogonal dimension, in this direction over here, you would find that there's very little variation in the second dimension, so if you only graphed your data along one dimension you'd be doing well.

Now this is an example of unsupervised learning where you find structure in terms of lower dimensionality of data. And especially for very high dimensional data, like image data, this is an important technique. So I talk a little bit later in this unit about dimensionality reduction. So in this class we learn about clustering, dimensionality reduction, and we'll apply it to a number of interesting problems.

Terminology

So to start with some lingo about unsupervised learning. If you look at this as a probabilist, you're given data, and we typically assume the data is IID, which means identically distributed and independently drawn from the same distribution. So a good chunk of unsupervised learning seeks to recover the underlying -- the density of the probability distribution that generated the data. It's called density estimation. As we find out our methods for clustering are versions of density estimation using what's called mixture models. Dimensionality reduction is also a method for doing density estimation. And there are many others.

Unsupervised learning can be applied to find structure in data. One of the fascinating ones that I believe exists is called blind signals separation. Suppose you are given a microphone, and two people simultaneously talk, and you record the joint of both of those speakers. Blind source separation or blind signal separation addresses the question of can you recover those two speakers and filter the data into two separate streams, one for each speaker. Now this is a really complicated unsupervised learning task, but is one of the many things that don't require target signals as unsupervised learning yet make for really interesting learning problems. This can be construed as an example of what's called factor analysis where each speaker is a factor in the joint signal that your microphone records. There are many other examples of unsupervised learning. I will show you a few in a second.

Google Street View and Clustering

Here is one of my favourite examples of unsupervised learning -- one that is yet unsolved. At Google, I had the opportunity to participate in the building of Street View, which is a huge photographic database of many many streets in the world. As you dive into Street View you can get ground imagery of almost any location in the world -- like this house here that I chose at random. In these images there is vast regularities. You can go somewhere else and you'll find that the type of objects visible in Street View is not entirely random. For example, there is many images of homes, many images of cars, trees, pavement, lane markers, stop signs, just to name a few. So one of the fascinating unsolved unsupervised learning tasks is: can you take hundreds of billions of images as comprised in the Street View data set and discover from it that there are concepts such as trees, lane markers, stop signs, cars and pedestrians? It seems to be tedious to hand label each image for the occurrence of such objects. And attempts to do so has resulted in very small image data sets. Humans can learn from data even without explicit target labels. We often just observe. In observing we apply unsupervised learning techniques. So one of the great, great open questions of artificial intelligence is: can you observe many intersections and many streets and many roads and learn from it what concepts are contained in the imagery?

Of course I can't teach you anything as complex in this class. I don't even know the answer myself. So let me start with something simple. Clustering. Clustering is the most basic form of unsupervised learning. And I will tell you about two algorithms that are very related. One is called k-means, and one is called expectation maximisation. K-means is a nice, intuitive algorithm to derive clusterings. Expectation maximisation is a probabilistic generalisation of k-means. They will be derived from first principles.

k-Means Clustering Example

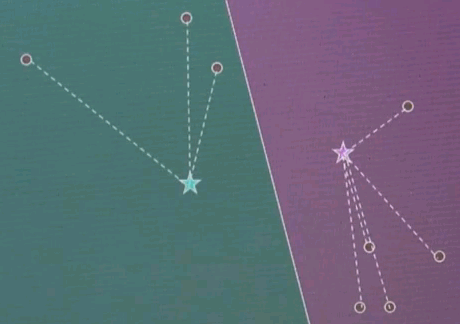
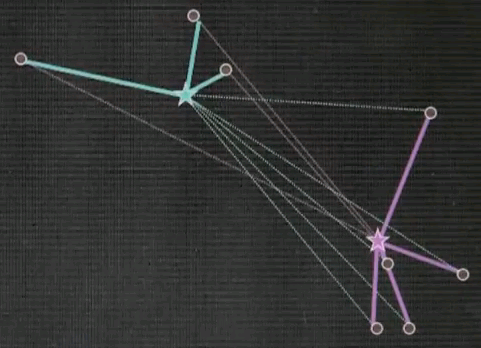
Let me explain k-means by an example. Suppose we're given the following data points in a two-dimensional space. K-means estimates for a fixed number of k, here k=2. The best centres of clusters representing those data points. Those are found iteratively by the following algorithm.

Step 1: Guess cluster centres at random, as shown over here with the two stars.

Step 2: Assign to each cluster centre, even though they are randomly chosen, the most likely corresponding data points. This is done by minimising Euclidean distance. In particular, each cluster centre represents half of the space. And the line that separates the space between the left and right cluster centre is the equidistant line, often called a Voronoi graph.

All the data points on the left correspond to the red (green) cluster, and the ones on the right to the green (purple) cluster.

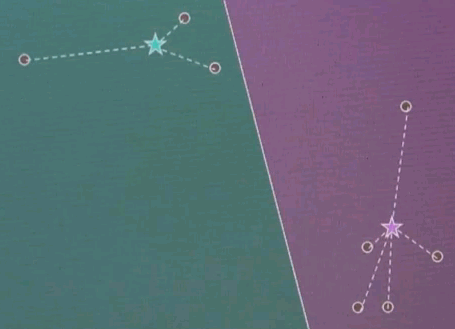
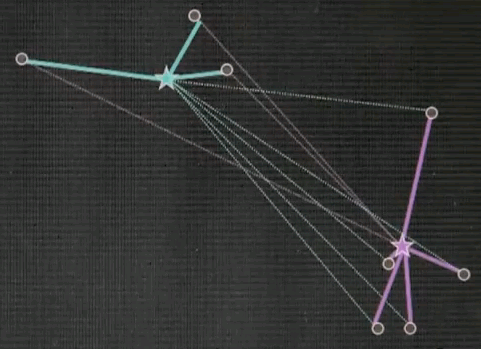
Step 3: Given now we have a correspondence between the data points and the cluster centres, find the optimal cluster centre that corresponds to the points associated with the cluster centre. Our red (green) cluster centre has only two data points attached. So the optimal cluster centre would be the halfway point in the middle.

Our right cluster centre has more than two data points attached, yet it isn't placed optimally, as you can see as they move with the animation back and forth. By minimising the joint quadratic distance to all of those points the new cluster centre is attained at the centre of those data points.

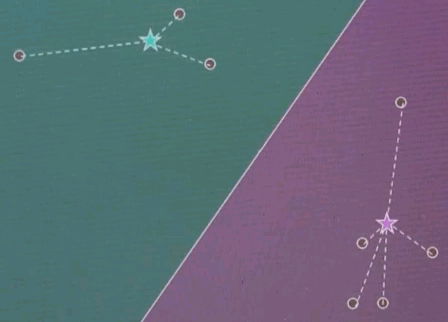
Now the final step is iterate. Go back and reassign cluster centres.

Now the Voronoi diagram has shifted, and the points are associated differently, and then re-evaluate what the optimal cluster centre looks like given the associated points.

And in both cases we see significant motion. Repeat.

Now this is the clustering. The point association doesn't change, and as a result, we just converged.

k-Means Algorithm

Note: For nearest distance, you may assume Euclidean. However, you can also generally substitute other distance metrics.

You just learned about an exciting clustering algorithm that's really easy to implement called k-means. To give you the algorithm in pseudocode initially we select k cluster centres at random and then we repeat. In a correspondence step, we correspond all the data points to the nearest cluster centre, and then we calculate the new cluster centre by the mean of the corresponding data points. We repeat this until nothing changes any more.

Now special care has to be taken if a cluster centre becomes empty -- that means no data point is associated. In which case we just restart cluster centres at random that have no corresponding points. Empty cluster centres restart at random.

This algorithm is known to converge to a locally optimal clustering of data points. The general clustering problem is known to be NP-hard. So a locally optimal solution, in a way, is the best we can hope for. Now let me talk about problems with k-means. First we need to know k, the number of cluster centres. As I mentioned, the local minima. For example, for four data points like this and two cluster centres that happen to be just over here, with the separation line like this, there would be no motion of k-means, even though moving one over here and one over there would give a better solution.

There's a general problem of high dimensionality of the space that is not dissimilar from the way k-nearest neighbour suffers from high dimensionality. And then there's lack of mathematical basis. Now if you're a practitioner, you might not care about a mathematical basis, but for the sake of this class, let's just care about it.

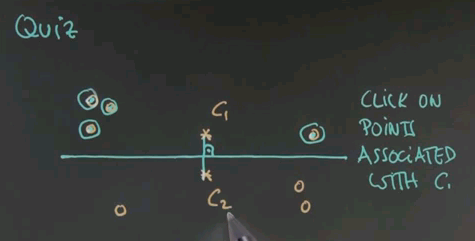
So here's a first quiz for k-means. Given the following two cluster centres, c₁ and c₂, click on exactly those points that are associated with c₁ and not with c₂.

And the answer is these four points over here. The reason is, if you draw the line of equal distance between c₁ and c₂, the separation of these two cluster areas falls over here. c₂ is down there, c₁ is up here.

Question

So here's my second quiz. Given the association we just derived for c₁, where do you think the new cluster centre, c₁, will be found after a single step of estimating its best location given the associated points? I'll give you a couple of choices. Please click on the one that you find the most plausible.

And the answer is over here. These four data points are associated with c₁, so we can safely ignore all the other ones. This one over here would be at the centre of the three data points over here, but this one pulls back this data point drastically towards it. This is about the best trade-off between these three points over here that all have a string attached and pull in this direction, compared to this point over here. Any of the other ones don't even lie between those points and therefore won't be good cluster centres. The one over here is way too far to the right.

Question

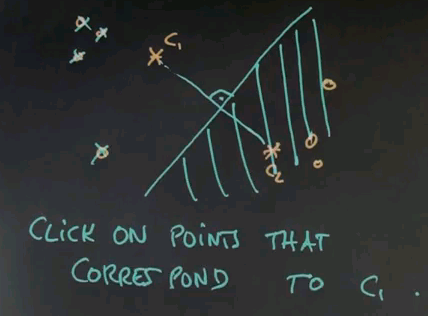
In our next quiz let's assume we've done one iteration and the cluster centre of c₁ moved over there and c₂ moved over here. Can you once again click on all those data points that correspond to c₁?

And the answer is now simple. It's this one over here. This one, this one, and this one. And the reason is, the line separating both clusters runs around here. That means all the area over here is c₂ territory, and the area over here is c₁ territory.

Obviously as we now iterate k-means, these clusters that have been moved straight over here will be able to stay, whereas, c₂ will end up somewhere over here.

Expectation Maximisation

So, let's now generalise k-means into expectation maximisation.

Expectation maximisation is an algorithm that uses actual probability distributions to describe what we're doing, and it's in many ways more general, and it's also nice in that it really has a probabilistic basis.

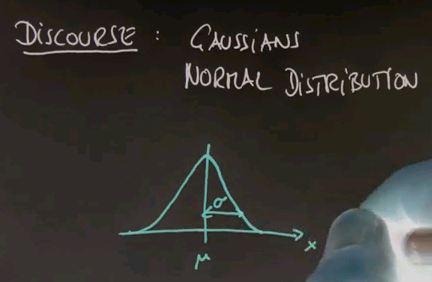
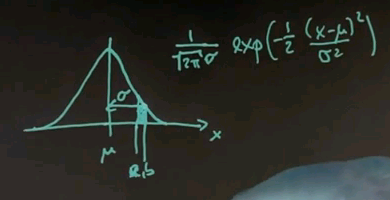
To get there, I have to take the discourse and tell you all about Gaussians, or the normal distribution, and the reason is so far we've just encountered discrete distributions, and Guassians will be the first example of a continuous distribution. Many of you know that a Gaussian is described by an identity that looks as follows, where the mean is called mu, and the variance is called sigma or sigma squared.

And for any x along the horizontal axis, the density is given by the following function: 1 over square root of 2 pi times sigma, and then an exponential function of minus a half of x minus mu squared over sigma squared.

This function might look complex, but it's also very, very beautiful. It peaks at x equals mu, where the value in the exponent becomes zero, and towards plus or minus infinity it goes to zero quickly. In fact, exponentially fast. The argument inside is a quadratic function. The exponential function makes it exponential. And this over here is a normaliser to make sure that the area underneath sums up to one, which is a characteristic of any probability density function.

If you map this back to our discrete random variables, for each possible x, we can now assign a density value, which is the function of this, and that's effectively the probability that this x might be drawn. Now the space itself is infinite, so any individual value will have a probability of zero, but what you can do is you can make an interval, A and B, and the area underneath this function is the total probability that an experiment will come up between A and B. Clearly it's more likely to generate values around mu than it is to generate values in the periphery somewhere over here.

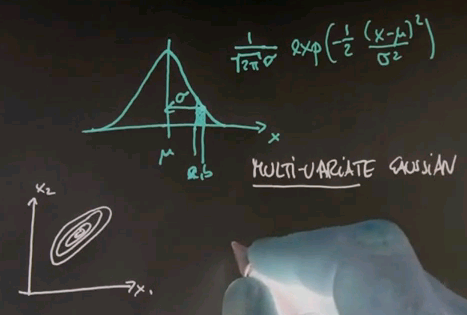
And just for completeness, I'm going to give you the formula for what's called the multivariate Gaussian, where multivariate means nothing else but we have more than one input variable. You might have a Gaussian over a two-dimensional space or a three-dimensional space. Often these Gaussians are drawn by what's called level sets, sets of equal probability. Here's one in a two-dimensional space, x₁ and x₂.

The Gaussian itself can be thought of as coming out of the paper towards me, where the most likely or highest point of probability is the centre over here. And these rings measure areas of equal probability.

The formula for a multivariate Gaussian looks as follows. N is the number of dimensions in the input space. Sigma is a covariance matrix that generalises the value over here. And the inner product inside the exponential is now done using linear algebra where this is the difference between a probe point and the mean vector mu transposed sigma to the minus 1 times x minus mu.

You can find this formula in any textbook or web page on Gaussians or multivariate normal distributions. It looks cryptic at first, but the key thing to remember is that it's just a generalisation of the one-dimensional case. We have a quadratic area over here as manifested by the product of this guy and this guy. We have a normalisation by a variance or covariance as shown by this number over here or the inverse matrix over here. And then this entire thing is an exponential form in both cases, and the normaliser looks a little more different in the multivariate case, but all it does is make sure that the volume underneath adds up to 1 to make it a legitimate probability density function.

For most of this explanation, I will stick with one-dimensional Gaussians, so all you have to do is to worry about this formula over here, but this is given just for completeness.

Gaussian Learning

Note: The formula is missing a minus sign: f ( x,mu,sigma^2 ) = 1 / ( sqrt (2 * pi * sigma^2) * exp ( -(x-mu)^2 / ( 2 * sigma^2 )

I will now talk about fitting Gaussians to data or Gaussian learning. You may be given some data points, and you might worry about what is the best Gaussian fitting the data? Now, to explain this, let me first tell you what parameters characterises a Gaussian. In the one-dimensional case, it is mu and sigma squared. Mu is the mean, sigma squared is called the variance. So if we look at the formula of a Gaussian, it's a function over any possible input x, and it requires knowledge of mu and sigma squared. And as before, I'm just restating what I said before, we get this function over here that specifies any probability for a value x given specific mu and sigma squared.

So suppose we wish to fit data, and our data is one-dimensional, and it looks as follows.

Just looking at this diagram makes me believe that there's a high density of data points over here and a fading density of data points over there, so maybe the most likely Gaussian will look a little bit like this where this is mu and this is sigma.

There are really easy formulas for fitting data to Gaussians, and I'll give you the result right now. The optimal or most likely mean is just the average of the data points. So there's M data points, x<sub1 to x_M. The average will look like this. The sum of all data points divided by the total number of data points.

That's called the average. And once you calculate the average, the sigma squared is obtained by a similar normalisation in a slightly more complex sum.

We sum the deviation from the mean and compute the average deviation to the square from the mean, and that gives us sigma squared. So, intuitively speaking, the formulas are really easy. Mu is the mean, or the average. Sigma squared is the average quadratic deviation from the mean, as shown over here.

Maximum Likelihood

Now I want to take a second to convince ourselves this is indeed the maximum likelihood estimate of the mean and the variance. Suppose our data looks like this -- there's M data points. And the probability of those data points for any Gaussian model -- mu and sigma squared is the product of any individual data likelihood x_i. And if you plug in our Gaussian formula, you get the following.

This is the normaliser multiplied M times where the square root is now drawn into the half over here. And here is our joint exponential, where we took the product of the individual exponentials and moved it up straight in here where it becomes a sum. So the best estimates for mu and sigma squared are those that maximise this entire expression over here for a given data set x₁ to x_m.

So we seek to maximise this over the unknown parameters mu and sigma squared. And now I will apply a trick. Instead of maximising this expression, I will maximise the logarithm of this expression. The logarithm is a monotonic function. So let's maximise instead the logarithm where this expression over here resolves to this expression over here. The multiplication becomes a minus sign from over here, and this is the argument inside the exponent written slightly differently but pulling the 2 sigma squared to the left.

So let's maximise this one instead. The maximum was obtained where the first derivative is zero. If we do this for our variable mu, we take the log f expression and compute the derivative with respect to mu, we get the following. This expression does not depend on mu at all, so it falls out. And we instead get this expression over here, which we've set to zero. And now we can multiply everything by sigma squared, it's still zero, and then bring the x_i to the right and the mu to the left. The sum over all E of the mu is mu equals sum over i, x_i.

Hence, we proved that the mean is indeed the maximum likelihood estimate for the Gaussian. This is now easily repeated for the variance. If you compute the derivative of this expression over here with respect to the variance, we get minus M over sigma, which happens to be the derivative of this expression over here. Keep in mind that the derivative of a logarithm is just its internal argument times by chain rule -- the derivative of the internal argument. Which if you work it out becomes this expression over here. And this guy over here changes signs but becomes the following. And again, you move this guy to the left side, multiply by sigma cubed, and divide by m. So we get the following result over here.

You might take a moment to verify these steps over here. I was a little bit fast, but this is relatively straight forward mathematics. And if you verify them you will find that the maximum likelihood estimate for sigma squared is the average deviation of data points from the mean mu. This gives us a very nice basis to fit Gaussians to data points.

So keeping these formulas in mind, here's a quick quiz, in which I ask you to actually calculate the mean and variance for a data sequence. So suppose the data you observe is 3, 4, 5, 6, and 7. There is 5 data points. Compute for me the mean and the variance using the maximum likelihood estimator I just gave you.

So the mean is obviously 5, it's the middle value over here. If I add those things together I get 25 and divide by 5. The average value over here is 5. The more interesting case is sigma squared, and I do this in the following steps. I subtract 5 from each of the data points for which I get -2, -1, 0, 1, and 2. I square those differences, which gives me 4, 1, 0, 1, 4. And now I compute the mean of those square differences. To do so I add them all up, which is 10. 10 divided by 5 is 2, and sigma squared equals 2.

Question

Here's another quiz. Suppose my data looks as follows -- 3, 9, 9, 3. Compute for me mu and sigma squared using the maximum likelihood estimator I just gave you.

And the answer is relatively easy. 3 + 9 + 9 + 3 = 24. Divided by m = 4 is 6. So the mean value is 6. Subtracting the mean from the data gives us -3, 3, 3, and -3. Squaring those gives us 9, 9, 9, 9 and the mean of four 9s equals 9.

Question

I now have a more challenging quiz for you in which I give you multivariate data, in this case two-dimensional data. So suppose my data goes as follows. In the first column I get 3, 4, 5, 6, 7. These are five data points and this is the first feature. And the second feature will be 8, 7, 5, 3, 2. The formulas for calculating mu and the covariance matrix sigma generalise the ones we studied before and they are given over here. So what I would like you to compute is the vector mu, which now has two values, on for the first and one for the second column and the variance sigma, which now has four different values, using the formula shown over here.

Now the mean is calculated as before independently for each of the two features here. 3, 4, 5, 6, 7; the mean is 5. 8, 7, 5, 3, 2; the mean is 5 again. Easy calculation. If you subtract the mean from the data we get the following matrix, and now we just have to plug it in. For the main diagonal elements you get the same formula as before. You can do this separately for each of the two columns. But for the off-diagonal elements you just have to plug it in. So this is the result after plugging it in and you might just want to verify it using a computer.

Gaussian Summary

So this finishes the lecture on Gaussians. You learned about what a Gaussian is. We talked about how to fit them from data, and we even talked about multivariate Gaussians. But even though I asked you to fit one of those the ones we're going to focus on right now is the one-dimensional Gaussian. So let's now move back to the expectation maximisation algorithm.

EM as Generalization of k-Means

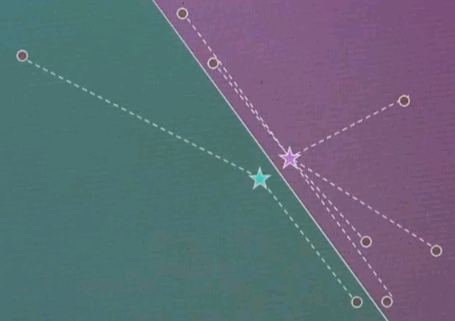
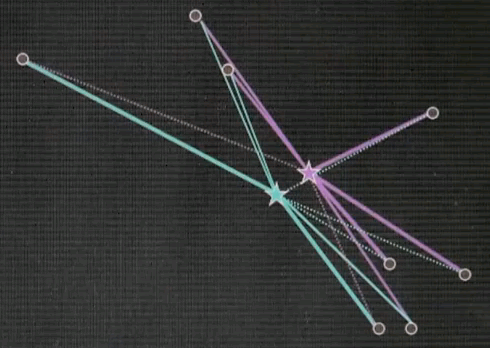
It is now really easy to explain expectation maximisation as a generalisation of k-means. Again we have a couple of data points here and two randomly chosen cluster centres.

But in the correspondence step instead of making a hard correspondence we make a soft correspondence.

Each data point is attracted to a cluster centre in proportion to the posterior likelihood which we will define in a minute. In the adjustment step, or the maximisation step, the cluster centres are being optimised just like before but now the correspondence is a soft variable and they correspond to all data points in different strengths not just the nearest ones.

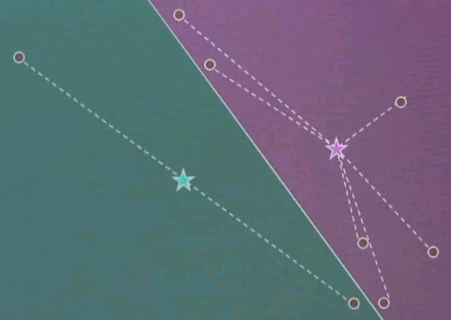
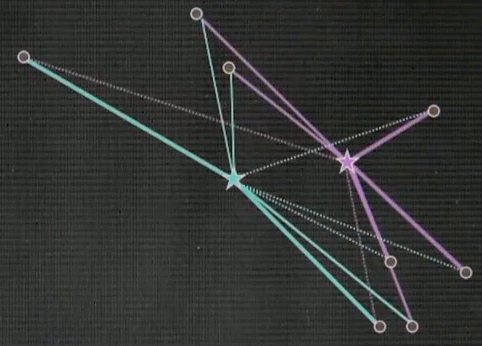
As a result, in EM the cluster centres tend not to move as far as in k-means. They move in a smoother way.

A new correspondence over here gives us different strength as indicated by the different colouring of the links and another relaxation step gives us better cluster centres.

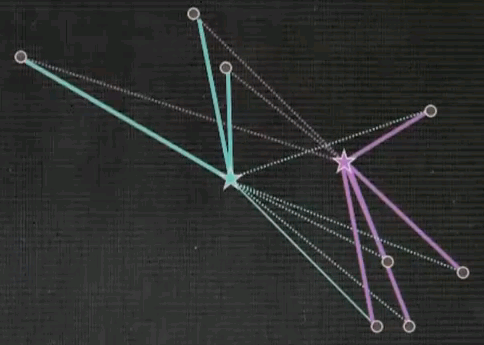
And as you can see, over time,

gradually the EM will then converge to about the same solution as k-means. However, all the correspondences are still alive. Which means there is not a 0, 1 correspondence, there is a soft correspondence which relates to a posterior probability, which I will explain next.

EM Algorithm

The model of expectation maximisation is that each data point is generated from what's called a mixture. The sum over all possible classes, or clusters, of which there are K, we draw a class at random with a prior probability of p of the class C=i and then we draw the data point x from the distribution correspondent with its class over here. The way to think about this, if there is K different cluster centres shown over here each one of those has a generic Gaussian attached. In the generative version of expectation maximisation you first draw a cluster centre and then we draw from the Gaussian attached to this cluster centre.

The unknowns here are the prior probabilities for each cluster centre

AI class unit 6

Contents

Unsupervised Learning