These are my notes for unit 6 of the AI class.

Unsupervised Learning

So welcome to the class on unsupervised learning. We talked a lot about supervised learning in which we are given data and target labels. In unsupervised learning we're just given data. So here is a data matrix of data items of n features each. There's m in total.

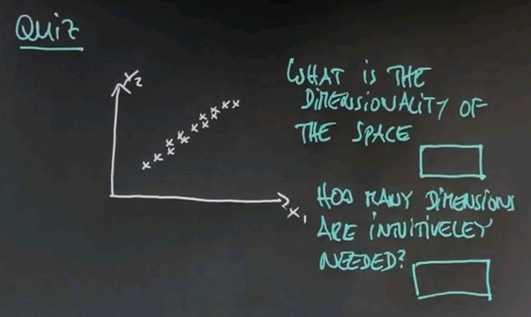
So the task of unsupervised learning is to find structure in data of this type. To illustrate why this is an interesting problem let me start with a quiz. Suppose we have two feature values. One over here, and one over here, and our data looks as follows. Even though we haven't been told anything in unsupervised learning, I'd like to quiz your intuition on the following two questions: First, is there structure? Or put differently do you think there's something to be learned about data like this, or is it entirely random? And second, to narrow this down, it feels that there are clusters of data the way I do it. So how many clusters can you see? And I give you a could of choices, 1, 2, 3, 4, or none.

The answer to the first question is yes, there is structure. Obviously these data seem not to be completely randomly determinate. There seem to be, for me, two clusters. So the correct answer for the second question is 2. There's a cluster over here, and there's a cluster over here. So one of the tasks of unsupervised learning will be to recover the number of clusters, and the centre of these clusters, and the variance of these clusters in data of the type I've just shown you.

Question

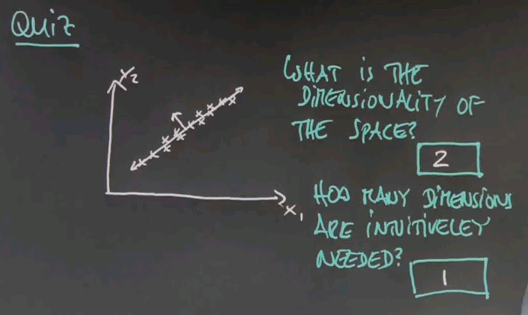
Let me ask you a second quiz. Again, we haven't talked about any details. But I would like to get your intuition on the following question. Suppose in a two-dimensional space all the data lies as follows. This may be reminiscent of the question I asked you for housing prices and square footage. Suppose we have two axes, x₁ and x₂. I'm going to ask you two questions here. One is what is the dimensionality of this space in which this data falls, and the second one is an intuitive question which is how many dimensions do you need to represent this data to capture the essence. And again, this is not a clear crisp 0 or 1 type question, but give me your best guess. How many dimensions are intuitively needed?

And here are the answers that I would give to these two questions. Obviously the dimensionality of the data is two, there's an x dimension and a y dimension. But I believe you can represent this all in one dimension. If you pick this dimension over here then the major variation of the data goes along this dimension. If you were for example to look at the orthogonal dimension, in this direction over here, you would find that there's very little variation in the second dimension, so if you only graphed your data along one dimension you'd be doing well.

Now this is an example of unsupervised learning where you find structure in terms of lower dimensionality of data. And especially for very high dimensional data, like image data, this is an important technique. So I talk a little bit later in this unit about dimensionality reduction. So in this class we learn about clustering, dimensionality reduction, and we'll apply it to a number of interesting problems.

Terminology

So to start with some lingo about unsupervised learning. If you look at this as a probabilist, you're given data, and we typically assume the data is IID, which means identically distributed and independently drawn from the same distribution. So a good chunk of unsupervised learning seeks to recover the underlying -- the density of the probability distribution that generated the data. It's called density estimation. As we find out our methods for clustering are versions of density estimation using what's called mixture models. Dimensionality reduction is also a method for doing density estimation. And there are many others.

Unsupervised learning can be applied to find structure in data. One of the fascinating ones that I believe exists is called blind signals separation. Suppose you are given a microphone, and two people simultaneously talk, and you record the joint of both of those speakers. Blind source separation or blind signal separation addresses the question of can you recover those two speakers and filter the data into two separate streams, one for each speaker. Now this is a really complicated unsupervised learning task, but is one of the many things that don't require target signals as unsupervised learning yet make for really interesting learning problems. This can be construed as an example of what's called factor analysis where each speaker is a factor in the joint signal that your microphone records. There are many other examples of unsupervised learning. I will show you a few in a second.

Google Street View and Clustering

Here is one of my favourite examples of unsupervised learning -- one that is yet unsolved. At Google, I had the opportunity to participate in the building of Street View, which is a huge photographic database of many many streets in the world. As you dive into Street View you can get ground imagery of almost any location in the world -- like this house here that I chose at random. In these images there is vast regularities. You can go somewhere else and you'll find that the type of objects visible in Street View is not entirely random. For example, there is many images of homes, many images of cars, trees, pavement, lane markers, stop signs, just to name a few. So one of the fascinating unsolved unsupervised learning tasks is: can you take hundreds of billions of images as comprised in the Street View data set and discover from it that there are concepts such as trees, lane markers, stop signs, cars and pedestrians? It seems to be tedious to hand label each image for the occurrence of such objects. And attempts to do so has resulted in very small image data sets. Humans can learn from data even without explicit target labels. We often just observe. In observing we apply unsupervised learning techniques. So one of the great, great open questions of artificial intelligence is: can you observe many intersections and many streets and many roads and learn from it what concepts are contained in the imagery?

Of course I can't teach you anything as complex in this class. I don't even know the answer myself. So let me start with something simple. Clustering. Clustering is the most basic form of unsupervised learning. And I will tell you about two algorithms that are very related. One is called k-means, and one is called expectation maximisation. K-means is a nice, intuitive algorithm to derive clusterings. Expectation maximisation is a probabilistic generalisation of k-means. They will be derived from first principles.

k-Means Clustering Example

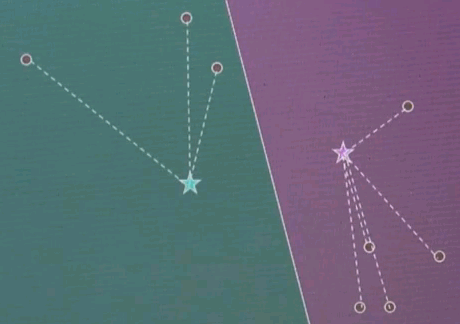
Let me explain k-means by an example. Suppose we're given the following data points in a two-dimensional space. K-means estimates for a fixed number of k, here k=2. The best centres of clusters representing those data points. Those are found iteratively by the following algorithm.

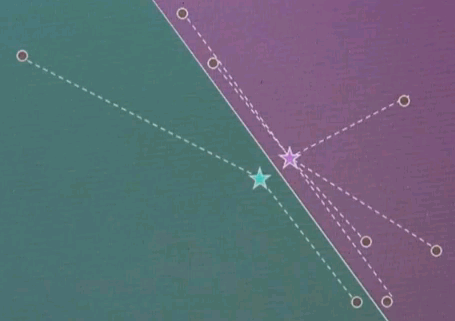
Step 1: Guess cluster centres at random, as shown over here with the two stars.

Step 2: Assign to each cluster centre, even though they are randomly chosen, the most likely corresponding data points. This is done by minimising Euclidean distance. In particular, each cluster centre represents half of the space. And the line that separates the space between the left and right cluster centre is the equidistant line, often called a Voronoi graph.

All the data points on the left correspond to the red (green) cluster, and the ones on the right to the green (purple) cluster.

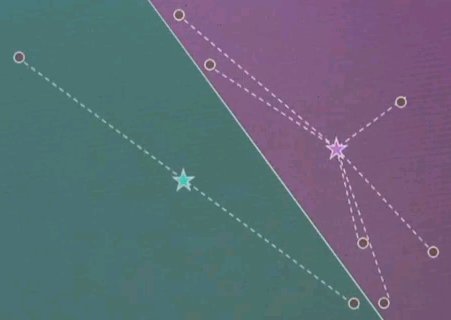
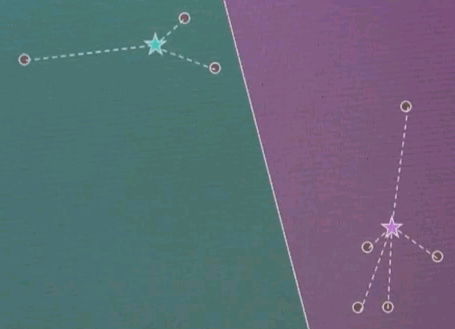
Step 3: Given now we have a correspondence between the data points and the cluster centres, find the optimal cluster centre that corresponds to the points associated with the cluster centre. Our red (green) cluster centre has only two data points attached. So the optimal cluster centre would be the halfway point in the middle.

Our right cluster centre has more than two data points attached, yet it isn't placed optimally, as you can see as they move with the animation back and forth. By minimising the joint quadratic distance to all of those points the new cluster centre is attained at the centre of those data points.

Now the final step is iterate. Go back and reassign cluster centres.

Now the Voronoi diagram has shifted, and the points are associated differently, and then re-evaluate what the optimal cluster centre looks like given the associated points.

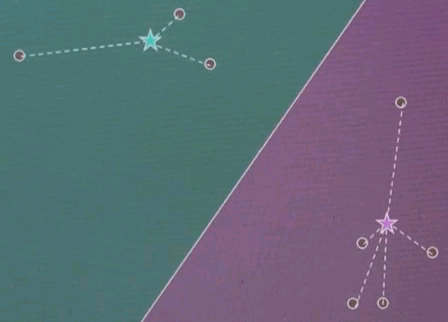
And in both cases we see significant motion. Repeat.

Now this is the clustering. The point association doesn't change, and as a result, we just converged.

AI class unit 6

Contents

Unsupervised Learning