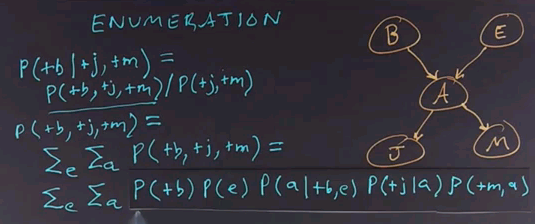AI class unit 4

These are my notes for unit 4 of the AI class.

Probabilistic Inference

Overview and Example

{{#ev:youtubehd|1fVWQ-iZqsw}}

Welcome back. In the previous unit, we went over the basics of probability theory and saw how a Bayes network could concisely represent a joint probability distribution, including the representation of independence between the variables. In this unit, we will see how to do probabilistic inference. That is, how to answer probability questions using Bayes nets.

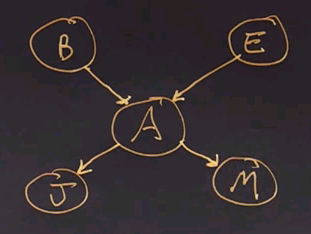
Let's put up a simple Bayes net. We'll use the familiar example of the earthquake where we can have a burglary (B) or an earthquake (E) setting off an alarm (A), and if the alarm goes off, either John (J) or Mary (M) might call.

Now, what kinds of questions can we ask to do inference about? The simplest type of question is the same question we ask with an ordinary subroutine or function in a programming language. Namely, given some inputs, what are the outputs? So, in this case, we could say given the inputs of B and E, what are the outputs J and M?

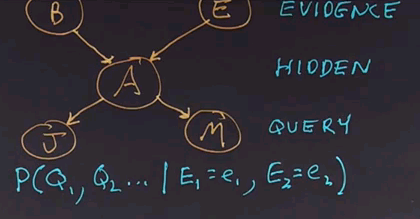
Rather than call them input and output variables, in probabilistic inference, we'll call them evidence and query variables. That is, the variables that we know the values of are the evidence, and the ones that we want to find out the values of are the query variables. Anything that is neither evidence nor query is known as a hidden variable. That is, we won't tell you what its value is. We won't figure out what its value is and report it, but we'll have to compute with it internally.

And now furthermore, in probabilistic inference, the output is not a single number for each of the query variables, but rather it's a probability distribution. So, the answer is going to be a complete, joint probability distribution over the query variables. We call this the posterior distribution, given the evidence, and we can write it like this:

It's the probability distribution of one or more query variables given the values of the evidence variables. And there can be zero or more evidence variables, and each of them are given an exact value. And that's the computation we want to come up with.

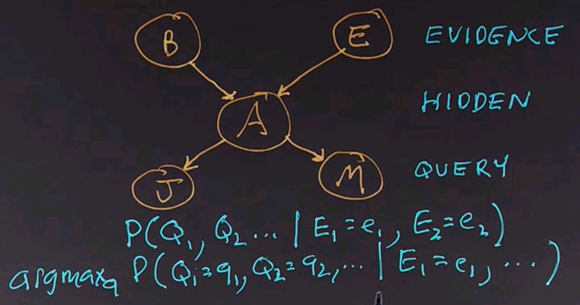
There's another question we can ask. Which is the most likely explanation? That is, out of all the possible values for all the query variables, which combination of values has the highest probability?

We write the formula like this:

asking which Q values are maximal given the evidence values. Now, in an ordinary programming language, each function goes only one way. It has input variables, does some computation, and comes up with a result variable or result variables. One great thing about Bayes nets is that we're not restricted to going only in one direction. We could go in the causal direction, giving as evidence the root nodes of the tree and asking as query values the nodes at the bottom. Or, we could reverse that causal flow. For example, we could have J and M be the evidence variables and B and E be the query variables, or we could have any other combination. For example, we could have M be the evidence variable and J and B be the query variables.

Here's a question for you. Imagine the situation where Mary has called to report that the alarm is going off, and we want to know whether or not there has been a burglary. For each of the nodes, click on the circle to tell us if the node is an evidence node, a hidden node, or a query node.

{{#ev:youtubehd|VYsys0If8bw}}

The answer is that Mary calling is the evidence node. The burglary is the query node, and all the others are hidden variables in this case.

Enumeration

{{#ev:youtubehd|VYsys0If8bw}}

Now we're going to talk about how to do inference on Bayes nets. We'll start with our familiar network, and we'll talk about a method called enumeration, which goes through all the possibilities, adds them up, and comes up with an answer.

So, what we do is start by stating the problem. We're going to ask the question of what is the probability that the burglar alarm occurred given that John called and Mary called? We'll use the definition of conditional probability to answer this.

So, this query is equal to the joint probability distribution of all 3 variables divided by the conditionalized variables. Now, note that I'm using a notation here where instead of writing out the probability of some variable equals true, I'm just using the notation plus and then the variable name in lower case, and if I wanted the negation, I would use the negation sign. Notice there's a different notation where instead of writing out the plus and negation signs, we just use the variable name itself, P(e), to indicate E is true.

That notation works well, but it can get confusing between does P(e) mean E is true, or does it mean E is a variable? And so we're going to stick to the notation where we explicitly have the pluses and negation signs.

To do inference by enumeration, we first take a conditional probability and rewrite it as unconditional probabilities. Now we enumerate all the atomic probabilities can calculate the sum of products. Let's look at just the complex term on the numerator first. The procedure for figuring out the denominator would be similar, and we'll skip that.

So, the probability of these three terms together can be determined by enumerating all possible values of the hidden variables. In this case there are 2, E and A. So we'll sum over those variables for all values of E and for all values of A. In this case they're boolean, so there's only two values of each. We ask what's the probability of this unconditional term? And that we get by summing out over all possibilities, E and A being true or false.

Now, to get the values of these atomic events, we'll have to rewrite this equation in a form that corresponds to the conditional probability tables that we have associated with the Bayes net. So, we'll take this whole expression and rewrite it. It's still a sum over the hidden variables E and A, but now I'll rewrite this expression in terms of the parents of each of the nodes in the network. So, that gives us the product of these five terms, which we then have to sum over all values of E and A.

If we call this product f(e,a), then the whole answer is the sum of F for all values of E and A, so it's the sum of four terms where each of the terms is a product of five numbers.

Where do we get the numbers to fill in this equation?