2011-AI

These are my notes from Sebastian Thrun and Peter Norvig's AI class. A course on Artificial Intelligence.

• AI class overview for an overview
• AI class journal for my journal

Course undertaken October to December 2011. Here goes nothing. :P

Week 1

Welcome to AI

Introduction

{{#ev:youtubehd|BnIJ7Ba5Sr4}}

Will deliver a good introduction to AI. Going to be a lot of work, but very rewarding.

New videos every week, and quizzes to test your knowledge built into the videos.

For the advanced version of the course are homework assignments and exams. These will be graded to determine if you can master AI the same way any good Stanford student could do it.

If you finish the course the lecturers will sign a letter of accomplishment and let you know what your rank in the class was.

Course Overview

{{#ev:youtubehd|Q7_GQq7cDyM}}

Purpose of the class:

• To teach the basics of AI artificial intelligence
• To excite you

Structure:

• Videos -> Quizzes -> Answer Videos
• Assignments (like quizzes but without the answers) and exams

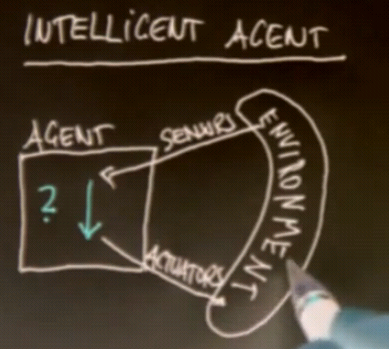
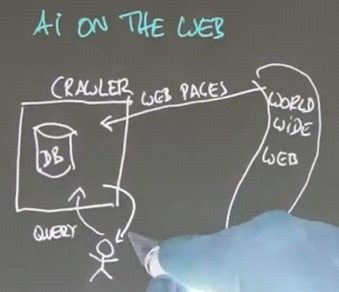
Intelligent Agents

{{#ev:youtubehd|cx3lV07w-XE}}

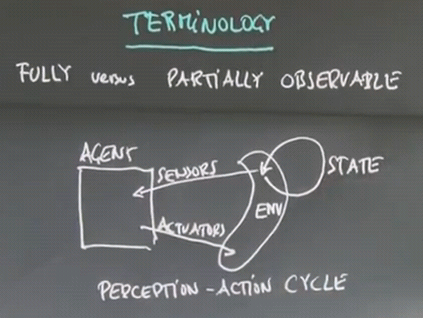
The agent has sensors that measure the environment, and actuators that can affect the environment.

The function that maps sensors to actuators is called the Control Policy of the agent.

This is the Perception-Action cycle:

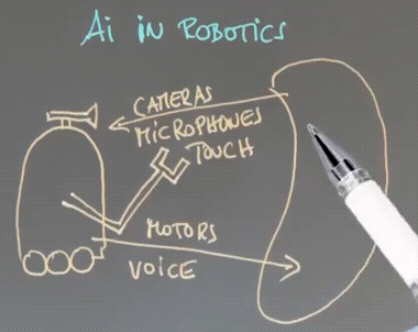
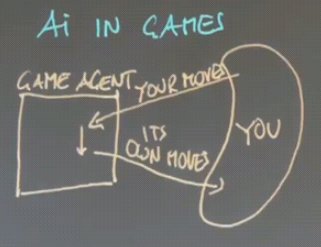
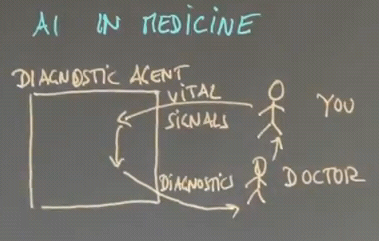
Applications of AI

{{#ev:youtubehd|N6JW8TQzbX8}}

Terminology

{{#ev:youtubehd|5lcLmhsmBnQ}}

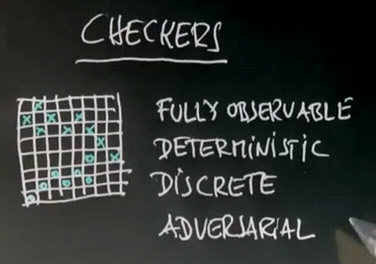
Checkers

{{#ev:youtubehd|qVppDRbx2kM}}

Poker Question

{{#ev:youtubehd|M_AdFAazf4k}}

{{#ev:youtubehd|DjILhASM3A8}}

Robot Car Question

{{#ev:youtubehd|vz-ERydsKLU}}

{{#ev:youtubehd|nOWCfVG0xNQ}}

AI and Uncertainty

{{#ev:youtubehd|ytw6_8a5Wls}}

Machine Translation

{{#ev:youtubehd|sPSN0aI0PgE}}

Chinese Translation

{{#ev:youtubehd|RWhwKudtixY}}

{{#ev:youtubehd|vvyaXxjsxBU}}

{{#ev:youtubehd|lFJey0tOvBg}}

Summary

{{#ev:youtubehd|mXM38kjzK-M}}

Problem Solving

Introduction

{{#ev:youtubehd|ZQmJuHtpGfs}}

In this unit we talk about problem solving. The theory and technology of building agents that can plan ahead to solve problems. In particular we're talking about problem solving where the complexity of the problem comes from the idea that there are many states, as in this problem here:

A navigation problem where there's many choices to start with and the complexity comes from picking the right choice now and picking the right choice at the next intersection and the intersection after that. Stringing together a sequence of actions.

This is in contrast to the type of complexity shown in this picture:

Where the complexity comes from the partial observability, that we can't see through the fog where the possible paths are or we can't see the results of our actions or even the actions themselves are not known. This type of complexity will be covered in another unit.

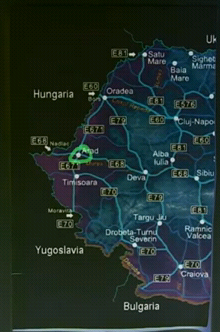
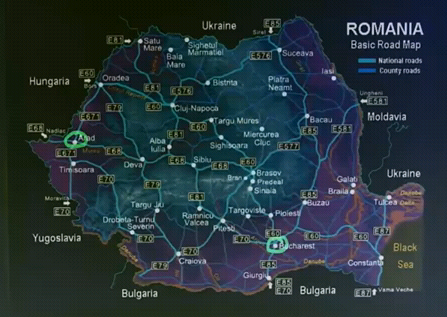
Here's an example of a problem:

This is a route finding problem. Where we are given start city Arad and a destination city Bucharest (the capital of Romania) and the problem then is to find a route from Arad to Bucharest. The actions that the agent can execute are driving from one city to the next along one of the roads shown on the map. The question is, is there a solution that the agent can come up with given the knowledge shown here to the problem of driving from Arad to Bucharest?

What is a Problem?

{{#ev:youtubehd|SIHc9LgMeaU}}

The answer is no. There is no solution that the agent could come up with, because Bucharest does not appear on the map. So the agent doesn't know any actions that can arrive there, so let's give the agent a better chance:

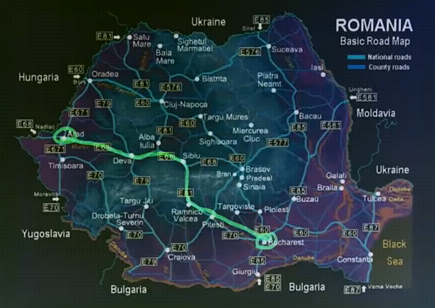
Now we've given the agent the full map of Romania. The start is in Arad; and the destination, or goal, is in Bucharest. The agent is given the problem of coming up with a sequence of actions that will arrive at the destination. Now is it possible for the agent to solve this problem?

The answer is yes, there are many routes, or steps, or sequences of actions, that will arrive at the destination, here is one of them:

Now let's formally define what a problem looks like. A problem can be broken down into a number of components.

First, the initial state that the agent starts out with. In our route finding problem the initial state was the agent being in the city of Arad.

Next, a function Actions that takes a state as input and returns a set of possible actions that the agent can execute when the agent is in this state. In some problems agents will have the same actions available in all states and in other problems they'll have different actions dependent on the state. In the route finding problem the actions are dependent on the state, when we're in one city we can take the routes to the neighbouring cities but we can't go to any other cities.

Next, we have a function called Result which takes as input a state and an action and delivers as its output a new state. So for example, if the agent is in the city of Arad (that would be the state) and takes the action of driving along route E671 toward Timisoara then the result of applying that action in that state would be the new state where the agent is in the city of Timisoara.

Next we need a function called GoalTest which takes a state and returns a boolean value (true or false) telling us if this state is a goal or not. In a route finding problem the only goal would be being in the destination city, the city of Bucharest, and all the other states would return false for the GoalTest.

Finally we need one more thing, which is a PathCost function, which takes a path, a sequence of state-action transitions, and returns a number which is the cost of that path. Now for most of the problems that we deal with we'll make the PathCost function be additive so that the cost of a path is just the sum of the cost of the individual steps. So we'll implement this PathCost function in terms of a StepCost function. The StepCost function takes a state, and action, and the resulting state from that action, and returns a number n which is the cost of that action. In the route finding example the cost might be the number of miles travelled or maybe the number of minutes it takes to get to that destination.