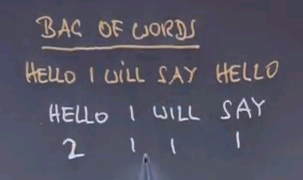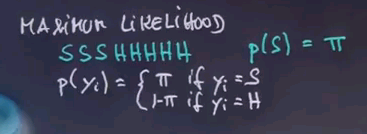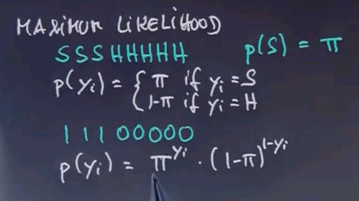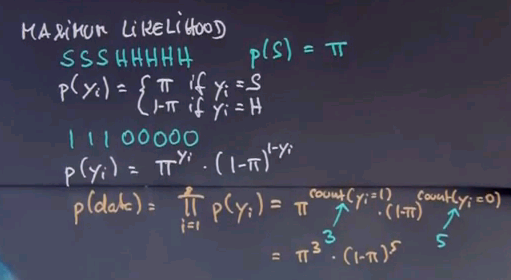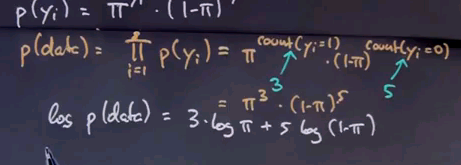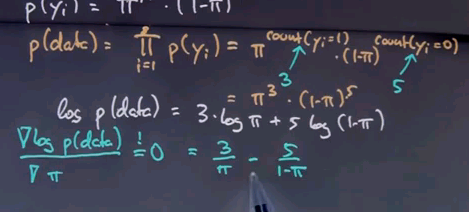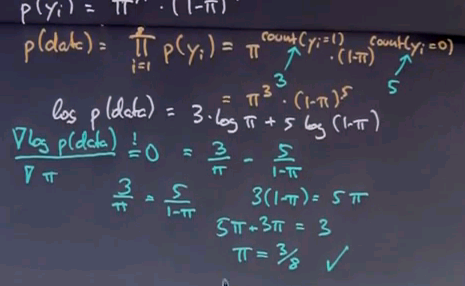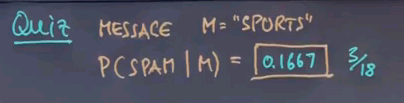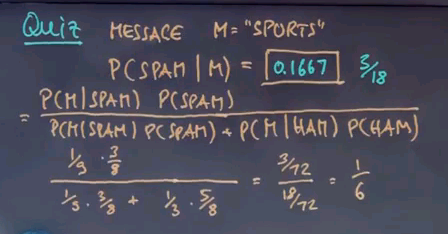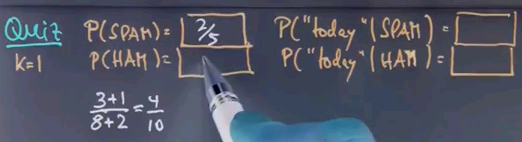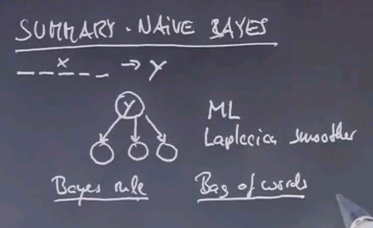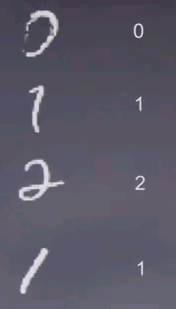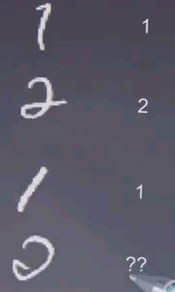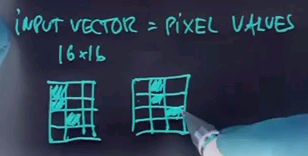AI class unit 5

These are my notes for unit 5 of the AI class.

Machine Learning

Introduction

{{#ev:youtubehd|8o1fAcyhap4}}

Welcome to the machine learning unit. Machine learning is a fascinating area. The world has become immeasurably data-rich. The world wide web has come up over the last decade. The human genome is being sequenced. Vast chemical databases, pharmaceutical databases, and financial databases are now available on a scale unthinkable even five years ago. To make sense out of the data, to extract information from the data, machine learning is the discipline to go.

Machine learning is an important sub-field of artificial intelligence, it's my personal favourite next to robotics because I believe it has a huge impact on society and is absolutely necessary as we move forward.

So in this class, I teach you some of the very basics of machine learning, and in our next unit Peter will tell you some more about machine learning. We'll talk about supervised learning, which is one side of machine learning, and Peter will tell you about unsupervised learning, which is a different style. Later in this class we will also encounter reinforcement learning, which is yet another style of machine learning. Anyhow, let's just dive in.

What is Machine Learning?

{{#ev:youtubehd|tEzGdI9nQt4}}

Welcome to the first class on machine learning. So far we talked a lot about Bayes Networks. And the way we talked about them is all about reasoning within Bayes Networks that are known. Machine learning addresses the problem of how to find those networks or other models based on data. Learning models from data is a major, major area of artificial intelligence and it's perhaps the one that had the most commercial success. In many commercial applications the models themselves are fitted based on data. For example, Google uses data to understand how to respond to each search query. Amazon uses data to understand how to place products on their website. And these machine learning techniques are the enabling techniques that make that possible.

So this class which is about supervised learning will go through some very basic methods for learning models from data, in particular, specific types of Bayes Networks. We will complement this with a class on unsupervised learning that will be taught next after this class.

Let me start off with a quiz. The quiz is: What companies are famous for machine learning using data? Google for mining the web. Netflix for mining what people would like to rent on DVDs. Which is DVD recommendations. Amazon.com for product placement. Check any or all and if none of those apply check down here.

{{#ev:youtubehd|SnbvK3_ayWI}}

And, not surprisingly, the answer is all of those companies and many, many more use massive machine learning for making decisions that are really essential to their businesses. Google mines the web and uses machine learning for translation, as we've seen in the introductory level. Netflix has used machine learning extensively for understanding what type of DVD to recommend to you next. Amazon composes its entire product pages using machine learning by understanding how customers respond to different compositions and placements of their products, and many, many other examples exist. I would argue that in Silicon Valley, at least half the companies dealing with customers and online products do extensively use machine learning. So it makes machine learning a really exciting discipline.

Stanley DARPA Grand Challenge

{{#ev:youtubehd|Q1xFdQfq5Fk}}

In my own research, I've extensively used machine learning for robotics. What you see here is a robot my students and I built at Stanford called Stanley, and it won the DARPA Grand Challenge. It's a self-driving car that drives without any human assistance whatsoever, and this vehicle extensively uses machine learning.

The robot is equipped with a laser system. I will talk more about lasers in my robotics class, but here you can see how the robot is able to build 3D models of the terrain ahead. These are almost like video game models that allow it to make assessments where to drive and where not to drive. Essentially it's trying to drive on flat ground.

The problem with these lasers is that they don't see very far. They only see about 25 meters out, so to drive really fast the robot has to see further, and this is where machine learning comes into play. What you see here is camera images delivered by the robot superimposed with laser data that doesn't see very far, but the laser is good enough to extract samples of driveable road surface that can then be machine learned and extrapolated into the entire camera image. That enables the robot to use the camera to see driveable terrain all the way to the horizon up to like 200 meters out, enough to drive really, really fast. This ability to adapt its vision by driving its own training examples using lasers but seeing out 200 meters or more was a key factor in winning the race.

Taxonomy

{{#ev:youtubehd|m-hcAePIkWY}}

Machine learning is a very large field with many different methods and many different applications. I will now define some of the very basic terminology that is being used to distinguish different machine learning methods.

Let's start with the what. What is being learned? You can learn parameters like the probabilities of a Bayes Network. You can learn structure like the arc structure of a Bayes Network. And you might even discover hidden concepts. For example, you might find that certain training examples form a hidden group. For example, Netflix might find that there's different types of customers some that care about classic movies some of them care about modern movies and those might form hidden concepts whose discovery can really help you make better sense of the data.

Next is what from? Every machine learning method is driven by some sort of target information that you care about. In supervised learning which is the subject of today's class we're given specific target labels and I'll give you examples in just a second. We also talk about unsupervised learning where target labels are missing and we use replacement principles to find, for example hidden concepts. Later there will be a class on reinforcement learning when an agent learns from feedback with the physical environment by interacting and trying actions and receiving some sort of evaluation from the environment like "Well done" or "That works." Again, we will talk about those in detail later.

There's different things you could try to do with machine learning techniques. You might care about prediction. For example you might want to care about what's going to happen with the future in the stockmarket for example. You might care to diagnose something which is you get data and you wish to explain it and you use machine learning for that. Sometimes your objective is to summarise something. For example if you read a long article your machine learning method might aim to produce a short article that summarises the long article. And there's many, many, many more different things.

You can talk about the how to learn. We use the word passive if your learning agent is just an observer and has no impact on the data itself. Otherwise we call it active. Sometimes learning occurs online which means while the data is being generated and some of it is offline which means learning occurs after the data has been generated.

There's different types of outputs of a machine learning algorithm. Today we'll talk about classification versus regression. In classification the output is binary or a fixed number of classes for example something is either a chair or not. Regression is continuous. The temperature might be 66.5 degrees in our prediction.

And there's tons of internal details we will talk about. Just to name one. We will distinguish generative from discriminative. Generative seeks to model the data as generally as possible versus discriminative methods seek to distinguish data and this might sound like a superficial distinction but has enormous ramification on the learning algorithm.

Now to tell you the truth it took me many years to fully learn all these words here and I don't expect you to pick them all up in one class but you should as well know that they exist. And as they come up I'll emphasise them so you can resort any learning method I tell you back into the specific taxonomy over here.

Supervised Learning

{{#ev:youtubehd|nxX9Ihi4HZQ}}

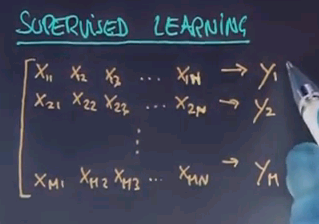
The vast amount of work in the field falls into the area of supervised learning. In supervised learning you're given for each training example a feature vector and a target label named Y. For example, for a credit rating agency X₁, X₂, X₃ might be a feature such as is the person employed? What is the salary of the person? Has the person previously defaulted on a credit card? And so on. And Y is a predictor whether the person is to default on the credit or not. Now machine learning is typically carried out on past data where the credit rating agency might have collected features just like these and actual occurrences of default or not. What it wishes to produce is a function that allows us to predict future customers. So when a new person comes in with a different feature vector, can we predict as good as possible the functional relationship between these features X₁ to X_n all the way to Y? You can apply the exact same example in image recognition where X might be pixels of images or it might be features of things found in images and Y might be a label that says whether a certain object is contained in an image or not.

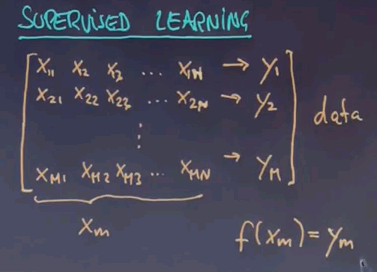
Now in supervised learning you're given many such examples. X₂₁ to X_2n leads to Y₂ all the way to index m.

This is called your data. If we call each input vector X_m and we wish to find out the function given any X_m or any future vector X produces as close as possible my target signal Y. Now this isn't always possible and sometimes it's acceptable, in fact preferable, to tolerate a certain amount of error in your training data. But the subject of machine learning is to identify this function over here.

And once you identify it you can use it for future Xs that weren't part of the training set to produce a prediction that hopefully is really, really good.

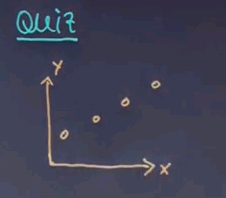
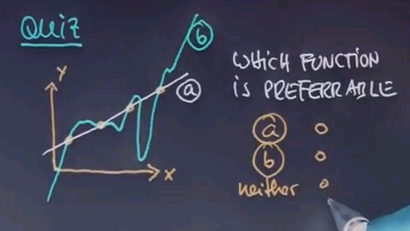
So let me ask you a question. And this is a question for which I haven't given you the answer but I'd like to appeal to your intuition. Here's one data set where the X is one dimensionally plotted horizontally and the Y is vertically and suppose that looks like this.

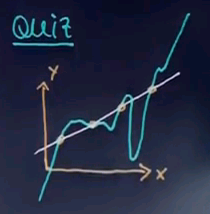
Suppose my machine learning algorithm gives me two hypotheses. One is this function over here which is a linear function and one is this function over here.

I'd like to know which of the functions you find preferable as an explanation for the data. Is it function A? Or function B?

Occam's Razor

{{#ev:youtubehd|FHJx9RVVKFg}}

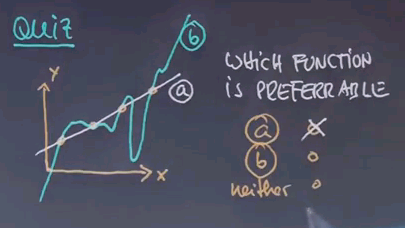
And I hope you guessed function A. Even though both perfectly describe the data B is much more complex than A. In fact, outside the data B seems to go to minus infinity much faster than these data points and to plus infinity much faster than with these data points over here. And in between we have wild oscillations that don't correspond to any data. So I would argue A is preferable.

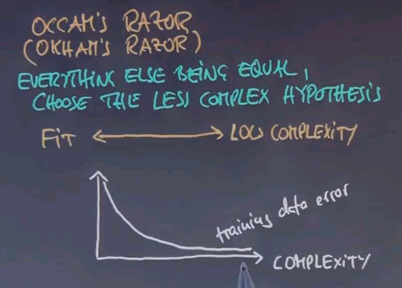
The reason why I asked this question is because of something called Occam's Razor. Occam can be spelled many different ways. And what Occam says is that everything else being equal choose the less complex hypothesis.

Now in practice there's actually a trade-off between a really good data fit and low complexity. Let me illustrate this to you by a hypothetical example. Consider the following graph where the horizontal axis graphs complexity of the solution. For example, if you use polynomials this might be a high-degree polynomial over here and maybe a linear function over here which is a low-degree polynomial. Your training data error tends to go like this.

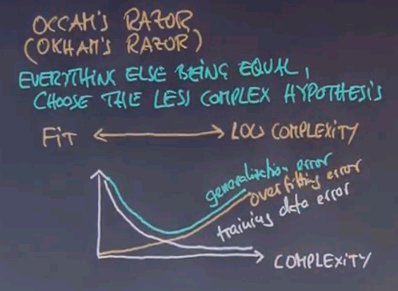
The more complex the hypothesis you allow the more you can just fit your data. However, in reality your generalisation error on unknown data tends to go like this. It is the sum of the training data error and another function which is called the overfitting error.

Not surprisingly the best complexity is obtained where the generalisation error is minimum. There are methods to calculate the overfitting error. They go into a statistical field under the name Bayes variance methods. However, in practice you're often just given the training data error. You find if you don't find the model that minimises the training data error but instead pushes back the complexity your algorithm tends to perform better and that is something we will study a little bit in this class.

However, this slide is really important for anybody doing machine learning in practice. If you deal with data and you have ways to fit your data be aware that overfitting is a major source of poor performance of a machine learning algorithm. And I'll give you examples in just one second.

SPAM Detection

{{#ev:youtubehd|wMMGexgmES4}}

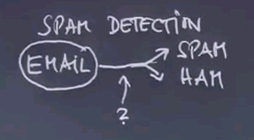
So a really important example of machine learning is SPAM detection. We all get way too much email and a good number of those are SPAM. Here are three examples of email. "Dear Sir: First I must solicit your confidence in this transaction, this is by virtue of its nature as being utterly confidential and top secret..." This is likely SPAM. Here's another one, in upper caps. "99 MILLION EMAIL ADDRESSES FOR ONLY $99" This is very likely SPAM. And here's another one. "Oh, I know this is blatantly OT but I'm beginning to go insane. Had an old Dell Dimension XPS sitting in the corner and decided to put it to use. I know it was working pre being stuck in the corner, but when I plugged it in, hit the power nothing happened." Now this is likely not SPAM.

How can a computer program distinguish between SPAM and not SPAM? Let's use this as an example to talk about machine learning for discrimination using Bayes Networks. In SPAM detection we get an email and we wish to categorise it either as SPAM in which case we don't even show it to the reader or what we call HAM which is the technical word for an email worth passing on to the person being emailed. So the function over here is the function we're trying to learn.

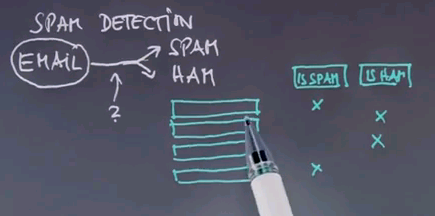
Most SPAM filters use human input. When you go through your email you have a button called "IS SPAM" which allows you as a user to flag SPAM and occasionally you will say an email is SPAM. If you look at this you have a typical supervised machine learning situation where the input is an email and the output is whether you flag it as SPAM or if we don't flag it we just think it's HAM.

Now to make this amenable to a machine learning algorithm we have to talk about how to represent emails. They're all using different words and different characters and they might have different graphics included. Let's pick a representation that's easy to process. And this representation is often called Bag of Words. Bag of Words is a representation of a document that just counts the frequency of words. If an email were to say "Hello I will say Hello." The Bag of Words representation is the following.

2-1-1-1 for the dictionary that contains the four words "Hello", "I", "will", "say". Now look at the subtlety here. Rather than representing each individual word we have a count of each word and the count is oblivious to the order in which the words were stated. A Bag of Words representation relative to a fixed dictionary represents the counts of each word relative to the words in the dictionary.

If you were to use a different dictionary like "Hello" and "Good-bye" our counts would be 2 and 0. However, in most cases you make sure that all the words found in messages are actually included in the dictionary. So the dictionary might be very, very large.

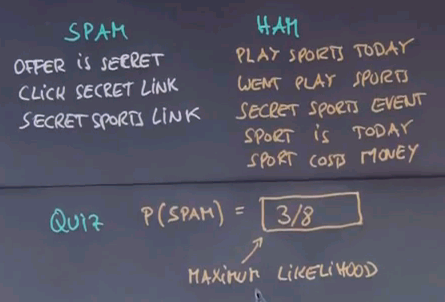
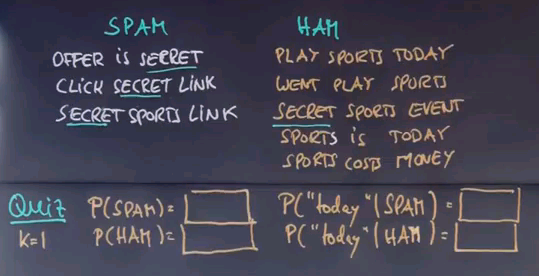
Let me make up an unofficial example of a few SPAM and a few HAM messages. "Offer is secret". "Click secret link". "Secret sports link". Obviously those are contrived and I tried to retain the vocabulary to a small number of words to make this example workable. In practice we need thousands of such messages to get good information. "Play sports today". "Went play sports". "Secret sports event". "Sport is today". "Sport costs money". My first quiz is: what is the size of the vocabulary that contains all words in these messages? Please enter the value in this box over here.

{{#ev:youtubehd|fPkxtmxRt5k}}

Well let's count. "Offer", "is", "secret", "click". "Secret" occurs over here already so we don't have to count it twice. "Link", "sports", "play", "today", "went", "event", "costs", "money". So the answer is 12. There's twelve different words contained in these eight messages.

Question

{{#ev:youtubehd|Diqx3Z20YWc}}

Another quiz. What is the probability that a random message that arrives will fall into the spam bucket? Assuming that those messages are all drawn at random.

{{#ev:youtubehd|WFE-dmEJZF8}}

And the answer is: there's eight different messages of which three are spam. So the maximum likelihood estimate is 3/8.

Maximum Likelihood 1

{{#ev:youtubehd|QBlERVSlFx4}}

Note: Assume the question is asking for the probability of a word in a spam message being "secret" NOT the probability that a spam message contains the word secret.

So, let's look at this a little bit more formally and talk about maximum likelihood. Obviously, we're observing eight messages: spam, spam, spam and five times ham. And what we care about is what's our prior probability of spam that maximises the likelihood of this data?

So, let's assume we're going to assign a value of pi to this, and we wish to find the pi that maximises the likelihood of this data over here, assuming that each email is drawn independently according to an identical distribution. The probability of the p(y_i) data item is then pi if y_i = spam, and 1 - pi if y_i = ham.

If we rewrite the data as 1,1,1,0,0,0,0,0, we can write p(y_i) as follows: pi to the y_i times (1 - pi) to the 1 - y_i.

It's not that easy to see that this is equivalent, but say y_i = 1. Then this term will fall out. It's a multiplication by 1 because the exponent is zero, and we get pi as over here. If y_i = 0, then this term falls out, and this one here becomes 1 - pi as over here.

Now assuming independence, we get for the entire data set that the joint probability of all data items is the product of the individual data items over here, which can now be written as follows:

pi to the count of instances where y_i = 1 times 1 - pi to the count of the instances where y_i = 0. And we know in our example, this count over here is three, and this count over here is five, so we get pi to the third times 1 - pi to the fifth.

We now wish to find the pi that maximises this expression over here. We can also maximise the logarithm of this expression, which is three times log pi + five times log (1 - pi).

Optimising the log is the same as optimising p because the log is monotonic in p. The maximum of this function is attained with a derivative of zero, so let's compute with a derivative and set it to zero. This is the derivative, 3 over pi - 5 over 1 - pi.

We now bring this expression to the right side, multiply the denominators up, and sort all the expressions containing pi to the left, which gives us pi = 3/8, exactly the number we were at before.

So we just derived mathematically that the data likelihood maximising number for the probability is indeed the empirical count, which means when we looked at this quiz before and we said a maximum likelihood for the prior probability of spam is 3/8, by simply counting 3 over 8 emails were spam, we actually followed proper mathematical principles to do maximum likelihood estimation. Now, you might not fully have gotten the derivation of this, and I recommend you to watch it again, but it's not that important for the progress in this class.

So, here's another quiz. I'd like the maximum likelihood, or ML solutions, for the following probabilities. The probability that the word "secret" comes up, assuming that we already know a message is spam, and the probability that the same word "secret" comes up if we happen to know the message is not spam, it's ham.

{{#ev:youtubehd|4q4Tk-4Long}}

And just as before we count the word secret in SPAM and in HAM as I've underlined here. Three out of nine words in SPAM are the word "secret" so we have a third over here, or 0.333, and only one out of all the fifteen words in HAM are "secret" so you get a fifteenth or 0.0667.

Relationship to Bayes Networks

{{#ev:youtubehd|MvwZNmJQIJw}}

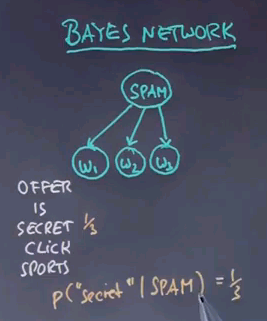
By now, you might have recognised what we're really building up is a Bayes network where the parameters of the Bayes networks are estimated using supervised learning by a maximum likelihood estimator based on training data.

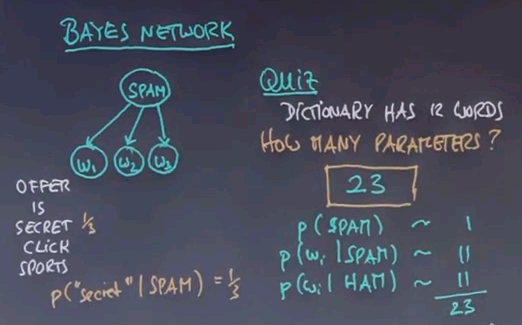
The Bayes network has at its root an unobservable variable called spam, which is binary, and it has as many children as there are words in a message, where each word has an identical conditional distribution of the word occurrence given the class spam or not spam. If you write down our dictionary over here -- you might remember the dictionary had twelve different words -- so here is five of the twelve, "offer", "is", "secret", "click" and "sports". Then for the spam class, we found the probability of "secret" given spam is 1/3, and we also found that the probability of "secret" given ham is 1/15.

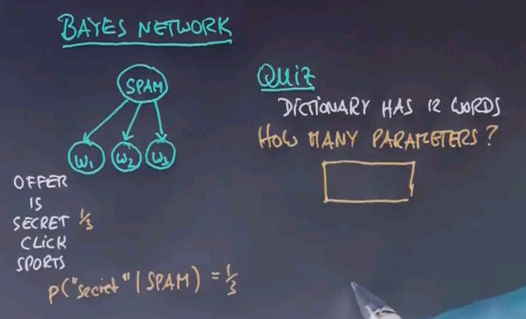
So here's a quiz. Assuming a vocabulary size of twelve, or put differently, the dictionary has twelve words, how many parameters do we need to specify this Bayes network?

{{#ev:youtubehd|-Pms2FiJQIA}}

And the correct answer is 23. We need one parameter for the prior p(spam), and then we have two dictionary distributions of any word i given spam, and the same for ham. Now, there's twelve words in a dictionary, but this distribution only needs eleven parameters, so twelve can be figured out because they have to add up to 1. And the same is true over here, so if you add all these together, we get 23.

Questions

{{#ev:youtubehd|2BFCqec6n04}}

So, here's a quiz. Let's assume we fit all the 23 parameters of the Bayes network as explained using maximum likelihood. Let's now do classification and see what class and message it ends up with. Let me start with a very simple message, and it contains a single word just to make it a little bit simpler. What's the probability that we classify this one word message as spam?

{{#ev:youtubehd|lQe4iNP6HDA}}

And the answer is 0.1667 or 3/18.

How do I get there? Well, let's apply Bayes rule. This form is easily transformed into this expression over here, the probability of the message given spam times the prior probability of spam over the normaliser over here. Now, we know that the word "sports" occurs 1 in our 9 words of spam, and our prior probability for spam is 3/8, which gives us this expression over here. We now have to add the same probabilities for the class ham. Sports occurs 5 times out of 15 in the ham class, and the prior probability for ham is 5/8, which gives us 3/72 divided by 18/72, which is 3/18 or 1/6.

{{#ev:youtubehd|qVdxj8XOB00}}

Let's do a more complicated quiz. Say the message now contains 3 words. "Secret is secret", not a particularly meaningful email, but the frequent occurrence of "secret" seems to suggest it might be spam. So what's the probability you're going to judge this to be spam?

{{#ev:youtubehd|eSbURIQ6pSQ}}

And the answer is surprisingly high. It's 25/26, or 0.9615. To see if we apply Bayes rule, which multiplies the prior for spam-ness with the conditional probability of each word given spam. "Secret" carries 1/3, "is" 1/9, and "secret" 1/3 again. We normalise this by the same expression plus the probability for the non-spam case. 5/8 as a prior. "Secret" is 1/15. "Is" is 1/15, and "secret" again. This resolves to 1/216 over this expression plus 1/5400, and when you work it all out is 25/26.

{{#ev:youtubehd|dfVAnFFxFP4}}

A final quiz. Let's assume our message is "Today is secret". Again, it might look like spam because the word "secret" occurs. I'd like you to compute for me the probability of spam given this message.

Laplace Smoothing

{{#ev:youtubehd|0BpC-cLDCIE}}

Note: At 2:20: count(x) is the number of occurrences of this value of the variable x. |x| is the number of values that the variable x can take on. k is a smoothing parameter. And N is the total number of occurrences of x (the variable, not the value) in the sample size.

And surprisingly, the probability for this message to be spam is 0. It's no 0.001. It's flat 0. In other words, it's impossible, according to our model, that this text could be a spam message. Why is this? Well when we apply the same rule as before, we get the prior for spam which is 3/8. And we multiply the conditional for each word into this. For "secret", we know it to be 1/3. For "is", to be 1/9, but for "today", it's 0. It's zero because the maximum of the estimate for the probability of "today" in spam is zero. "Today" just never occurred in a spam message so far. Now, this 0 is troublesome because as we compute the outcome -- and I'm plugging in all the numbers as before -- none of the words matter anymore, just the zero matters. So we get zero over something which is plain zero. Are we overfitting? You bet. We are clearly overfitting.

It can't be that a single word determines the entire outcome of our analysis. The reason is that our model, to assign a probability of zero for the word "today" to be in the class of spam is just too aggressive. So let's change this.

One technique to deal with the overfitting problem is called Laplace Smoothing. In maximum likelihood estimation, we assign towards our probability the quotient of the count of this specific event over all events in our data set. So for example, for the prior probability, we found that 3/8 messages are spam. Therefore, our maximum likelihood estimate for the prior probability of spam was 3/8. In Laplace Smoothing, we use a different estimate. We add the value k to the count and normalise as if we added k to every single class that we've tried to estimate something over.

This is equivalent to assuming we have a couple of fake training examples where we add k to each observation count. Now, if k equals 0, we get our maximum likelihood estimator. But if k is larger than 0 and n is finite, we get different answers. Let's set k equals 1, and let's assume we get one message, and that message was spam, so we're going to write it one message, one spam. What is p(spam) for the Laplace smoothing of k + 1? Let's do the same with 10 messages, and we get 6 spam. And 100 messages, of which 60 are spam. Please enter your numbers into the boxes over here.

{{#ev:youtubehd|2sKSZHkQPrc}}

The answer here is 2/3 or 0.667 and is computed as follows. We have 1 message with 1 as spam, but we're going to add k = 1. We're going to add k = 2 over here because there's 2 different classes. k = 1 times 2 equals 2, which gives us 2/3.

The answer over here is 7/12. Again, we have 6/10 but we add 2 down here and 1 over here, so you get 7/12.

And correspondingly, we get 61/102 is 60 + 1 over 100 + 2.

If we look at the numbers over here, we get 0.5833 and 0.5986.

Interestingly, the maximum likelihood on the last 2 cases over here will give us 0.6, but we only get a value that's closer to 0.5, which is the effect of our smoothing prior for the Laplacian smoothing.

Question

{{#ev:youtubehd|2Ar6jFKZhUM}}

Let's use the Laplacian smoother with k=1 to calculate a few interesting probabilities -- P(SPAM) and P(HAM) -- and then the probability of the words "today", given that it's in the SPAM class or the HAM class. And you might assume that our vocabulary size is about 12 different words here.

{{#ev:youtubehd|DjvGl1qRVdE}}

This one is easy to calculate for SPAM and HAM. For SPAM it's 2/5, and the reason is, we had previously 3 out of 8 messages assigned to SPAM, but thanks to the Laplacian smoother we add 1 over here, and there are 2 classes, so we add 2 times 1 over here, which gives us 4/10, which is 2/5.

Similarly we get 3/5 over here. Now the tricky part comes up over here. Before we had 0 occurrences of the word "today" in the SPAM class, and we had 9 data points. But now we're going to add 1 for Laplacian smoother, and down here we're going to add 12.

And the reason that we add 12 is because there's 12 different words in our dictionary. Hence, for each word in the dictionary we are going to add 1. So we have a total of 12, which gives us the 12 over here. That makes 1/21.

In the HAM class, we had 2 occurrences of the word "today" -- over here and over here. We add 1, normalise by 15, plus 12 for the dictionary size, which is 3/27 or 1/9.

This was not an easy question.

Question

{{#ev:youtubehd|RJAFdBfGOrY}}

We come now to the final quiz here, which is -- I would like to compute the probability that the message "today is secret" falls into the SPAM box with Laplacian smoother using k=1. Please just enter your number over here. This is a non-trivial question. It might take you a while to calculate this.

{{#ev:youtubehd|oh4uc-8O6Pc}}

And the approximate probability is 0.4858. How did we get this? Well, the prior probability for SPAM under the Laplacian smoothing is 2/5. "Today" doesn't occur, but we have already calculated this to be 1/21. "Is" occurs once, so we get 2 over here over 21. "Secret" occurs 3 times, so we get a 4 over here over 21, and we normalise this by the same expression over here, plus the prior for HAM, which is 3/5, we have 2 occurrences of "today", plus 1, equals 3/27. "Is" occurs once for 2/27. And "secret" occurs once, again, 2/27. When you work this all out, you get this number over here.

Summary Naive Bayes

{{#ev:youtubehd|c2yFCp6BrEA}}

So we learned quite a bit. We learned about Naive Bayes as our first supervised learning method. The setup was that we had features of documents or training examples. And labels, in this case, SPAM or not SPAM. And from those features we made a generative model for the SPAM class and the non-SPAM class that described the conditional probability of each individual feature. We then used first maximum likelihood and then a Laplacian smoother to fit those parameters over here. And then using Bayes rule we could take any training example over here and figure our what the class probability was over here. This is called a generative model in that the conditional probabilities all aim to maximise the probability of individual features as if those describe the physical world. We also used what's called a bag of words model, in which our representation of each email was such that we just counted the occurrences of words, irrespective of their order.

Now this is a very powerful method for fighting SPAM. Unfortunately, it's not powerful enough. It turns out spammers know about Naive Bayes, and they've long learned to come up with messages that are fooling your SPAM filter if it uses Naive Bayes. So companies like Google and others have become much more involved in methods for SPAM filtering. Now I can give you some more examples how to filter SPAM, but all of those quite easily fit with the same Naive Bayes model.

Advanced SPAM Filtering

{{#ev:youtubehd|GSHJspQH15c}}

So here are features that you might consider when you write an advanced spam filter. For example, does the email come from a known spamming IP or computer? Have you emailed this person before? In which case it is less likely to be spam. Here's a powerful one: have 1000 other people recently received the same message? Is the email header consistent? So for example if the from field says your bank is the IP address really your bank? Surprisingly is the email all caps? Strangely many spammers believe if you write things in all caps you'll pay more attention to it. Do the inline URLs point to those pages where they say they're pointing to? Are you addressed by your correct name?

Now these are some features, I'm sure you can think of more. You can toss them easily into the Naive Bayes model and get better classification. In fact modern spam filters keep learning as people flag emails as spam and of course spammers keep learning as well and trying to fool modern spam filters. Who's going to win? Well so far the spam filters are clearly winning. Most of my spam I never see, but who knows what's going to happen in the future..? It's a really fascinating machine learning problem.

Digit Recognition

{{#ev:youtubehd|kD2wD_MDVk4}}

Naive Bayes can also be applied to the problem of hand written digit recognition. This is a sample of hand-written digits taken taken from a U.S. postal data set where hand written zip codes on letters are being scanned and automatically classified.

The machine learning problem here is taking a symbol just like this, what is the corresponding number? Here it's obviously 0. Here it's obviously 1. Here it's obviously 2, 1. For the one down here it's a little bit harder to tell.

Now when you apply Naive Bayes, the input vector could be the pixel values of each individual pixel, so we have a 16 x 16 input resolution. You would get 156 different values corresponding to the brightness of each pixel. Now obviously given sufficiently many training examples you might hope to recognise digits, but one of the deficiencies of this approach is it's not particularly shift-invariant.

So, for example, a pattern like this will look fundamentally different from a pattern like this:

Even though the pattern on the right is obtained by shifting the pattern on the left by 1 to the right. There's many different solutions, but a common one could be to use smoothing in a different way from the way we discussed it before. Instead of just counting 1 pixel value's count, you could mix it with the counts of the neighbouring pixel values so if all pixels are slightly shifted, we get about the same statistics as the pixel itself. Such a method is called input smoothing. You can what's technically called convolve the input vector with the Gaussian variable, and you might get better results that if you do Naive Bayes on the raw pixels. Now to tell you the truth for digit recognition of this type, Naive Bayes is not a good choice. The conditional independence assumption of each pixel, given the class, is too strong an assumption in this case, but it's fun to talk about image recognition in the context of Naive Bayes regardless.

Overfitting Prevention

{{#ev:youtubehd|-jswWk8YLro}}

So, let me step back a step and talk a bit about overfitting prevention in machine learning, because it's such an important topic. We talked about Occam's Razor, which in a generalised way suggests there is a tradeoff between how well we can fit the data and how smooth our learning algorithm is. And in our class on smoothing, we already found one way to let Occam's Razor play, which is by selecting the value k to make our statistical counts smoother.

I alluded to a similar way in the image recognition domain where we smoothed the image so the neighbouring pixels count similar. This all raises the question of how to choose the smoothing parameter. So, in particular, in Laplacian smoothing, how to choose the k.

There is a method called cross-validation which can help you find an answer. This method assumes there is plenty of training examples, but to tell you the truth, in spam filtering there is more than you'd ever want.

Take your training data and divide it into three buckets. Train, cross-validate, and test. Typical ratios will be 80% goes into train, 10% into cross-validate, and 10% into test. You use the train to find all your parameters. For example, the probabilities of a Bayes network. You use your cross-validation set to find the optimal k, and the way you do this is you train for different values of k, you observe how well the training model performs on the cross-validation data, not touching the test data, and then you maximise over all the ks to get the best performance on the cross-validation set. You iterate this many times until you find the best k. When you're done with the best k, you train again, and then finally only once you touch the test data to verify the performance, and this is the performance you report.

It's really important in cross-validation to split apart a cross-validation set that's different from the test set. If you were to use the test set to find the optimal k, then your test set becomes and effective part of your training routine, and you might overfit your test data, and you wouldn't even know. By keeping the test data separate from the beginning, and training on the training data, you use the cross-validation data to find how good your training data is doing, under unknown parameters such as k, to fine-tune the k. And then finally, only once you use the test data, you get a fair answer to the question, "How well will your model perform on future data?"

So, pretty much everybody in machine learning uses this model. You can redo the split between training and the cross-validation part, people often use the word 10-fold cross-validation where they do 10 different foldings and run the model 10 times to find the optimal k or smoothing parameter. No matter which way you do it, find the optimal smoothing parameter, and then use a test set exactly once to verify and report.